Сумматор — это тип цифровой схемы в цифровой электронике, которая используется для выполнения операций сложения. Даже сама операция умножения во многом зависит от последовательности выполнения этой операции. Таким образом, их можно реализовать по-разному, с использованием разных технологий и разных диапазонов архитектур. Высокоскоростная и надежная конструкция сумматора является основной целью во встроенных приложениях и операциях фильтрации. Доступны различные типы сумматоров, например сумматор пульсирующего переноса , сумматор Когге-стоуна, сумматор связующего дерева, сумматор Брент-кунга, сумматор параллельных префиксов, сумматор переноса вперед, разреженный сумматор Когге-стоуна и т. д. В этой статье обсуждается обзор Когге Стоун Адде р или КСА.
Что такое каменная гадюка Когге?
Сумматор Когге-Стоуна или KSA представляет собой параллельную префиксную форму CLA (сумматор с упреждающим переносом) . Этот сумматор требует больше места для реализации по сравнению с сумматором Брента-Кунга, хотя он имеет небольшое разветвление на каждом этапе, что повышает производительность типичных узлов процесса CMOS. Однако перегруженность проводки часто является проблемой для KSA.
Сумматор Kogge Stone или KSA — это очень быстрый сумматор, используемый при различной обработке сигналов. процессоры (SPP) для наилучшего выполнения арифметических функций. Таким образом, скорость работы этого сумматора может быть ограничена путем распространения сигнала от входа к выходу. Как правило, KSA представляет собой параллельный префиксный сумматор, который обеспечивает лучшее сложение в зависимости от времени разработки и используется для высокопроизводительных арифметических схем в отрасли.
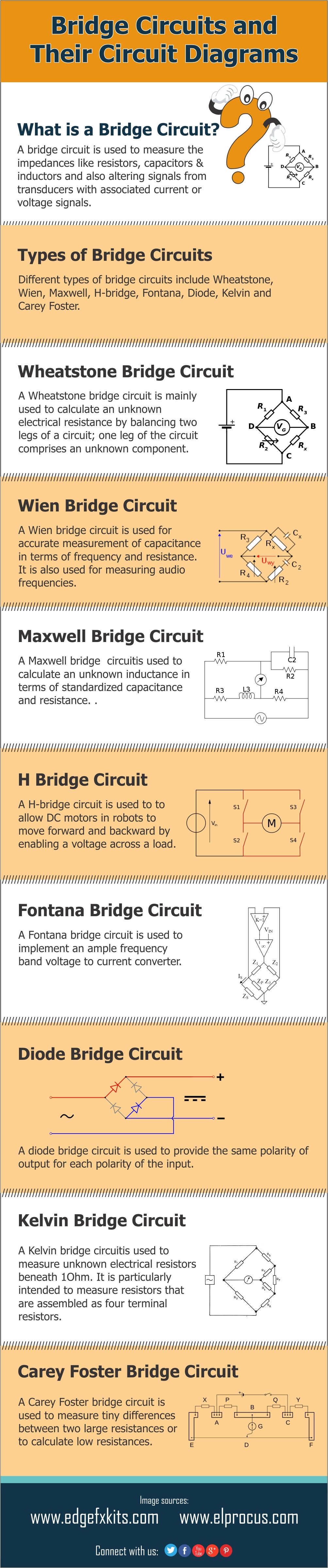
Принципиальная схема сумматора Kogge Stone
Схема сумматора Когге-Стоуна показана ниже. Этот тип сумматора считается просто самой быстрой и наиболее распространенной архитектурой сумматора, в основном для высокопроизводительных сумматоров в отрасли. В сумматорах этого типа несущие генерируются очень быстро путем их параллельного вычисления с увеличенной стоимостью площади.
Древовидные структуры распространения переноса и генерации сигналов показаны на диаграмме ниже. В этом сумматоре сеть генерации переносов представляет собой очень значимый блок, включающий три блока; Черная ячейка, серая ячейка и буфер. Таким образом, ячейки черного цвета используются в основном при расчете сигналов генерации и распространения, ячейки серого цвета в основном используются при расчете сигналов генерации, которые необходимы для расчета суммы на этапе постобработки, а буферы в основном используются для балансировки эффект загрузки.

Как работает каменная гадюка Когге?
Сумматор Когге-Стоуна отслеживает «генерацию» и «распространение» битов внутри для диапазонов битов, как и все сумматоры с упреждающим переносом. Мы начинаем с 1-битных интервалов, где один столбец в сложении создает бит переноса, когда оба входа равны 1 (логическое И), и бит переноса будет распространяться, если ровно один вход равен 1 (логическое исключающее ИЛИ). Таким образом, Kogge-Stone Adder включает в себя в основном три этапа обработки для вычисления битов суммы; этап предварительной обработки, сеть генерации переноса и этап постобработки. Таким образом, эти три шага в основном задействованы в операции суммирования. Эти три этапа обсуждаются ниже.

Этап предварительной обработки
Этот этап предварительной обработки включает в себя вычисление как генерируемых, так и распространяемых сигналов, эквивалентных каждой паре битов внутри A и B.
Пи = Ай х Би
Ги = Ай и Би
Сеть генерации керри
На этапе генерации переноса мы вычисляем переносы, эквивалентные каждому биту. Таким образом, выполнение этих операций может осуществляться параллельно. После параллельных вычислений переносов они сегментируются на мелкие части. В качестве промежуточных сигналов используются сигналы распространения переноса и генерации, которые определяются приведенными ниже логическими уравнениями.
CPi:j = Pi:k + 1 и Pk:j
CGi:j = Gi:k + 1 или (Pi:k + 1 и Gk:j)
Постобработка
Этот этап постобработки очень общий для всех сумматоров семейства с упреждающим переносом и включает в себя вычисление битов суммы.
Ci – 1 = (Pi и Cin) или Gi
Si = Pi = x или Ci – 1
4-битный сумматор Когге-Стоуна
В 4-битном сумматоре Когге-Стоуна каждая вертикальная ступень генерирует бит «распространения» и «генерации». Переносы генерируются на заключительном этапе, где эти биты подвергаются операции XOR при первом распространении после ввода в квадратных полях для генерации битов суммы.

Например; если распространение рассчитывается с помощью XOR, когда A = 1 и B = 0, тогда оно генерирует распространение o/p как 1. Здесь значение генерации может быть рассчитано с помощью AND, когда A = 1, B = 0, и генерируется значение Значение o/p равно 0. Аналогично, все биты суммы вычисляются для входов: A = 1011 и B = 1100. Выходы затем суммируются = 0111 и переносят Cout = 1. В этом сумматоре перейдите к пяти выходам в приведенном ниже расширении.
S0 = (A0^B0)^ 𝐶𝐼𝑁.
S1 = (А1 ^ В1) ^ (А0 и В0).
S2 = (A2 ^B2) ^ (((A1 ^ B1) & (A0 и B0)) | (A1 и B1)).
S3 = (A3 ^ B3) ^ ((((A2 ^ B2) & (A1 ^ B1)) & (A0 & B0)) | (((A2 ^ B2) & (A1 & B1)) | (A2 &
Б2))).
S4 = (A4 ^ B4) ^ ((((A3 ^ B3) & (A2 ^ B2)) & (A1 и B1)) | (((A3 ^ B3) & (A2 и B2)) | (A3 и B3) ))).
Преимущества и недостатки
Преимущества сумматора Kogge Stone включить следующее.
- Каменная сумматор Kogge — очень быстрая сумматор.
- Это расширенная версия для параллельных сумматоров префиксов.
- Этот сумматор помогает снизить энергопотребление, а также задержку по сравнению с другой логикой обычного типа.
- Он ориентирован на время разработки и лучше всего подходит для высокопроизводительных приложений.
- Этот сумматор стал очень эффективным в КИХ-фильтре по сравнению с другими типами сумматоров за счет значительного сокращения вычислительной мощности, площади и времени.
Недостатки сумматора Когге-камня включить следующее.
- Этот сумматор требует больше места для реализации по сравнению с сумматором Брента-Кунга, хотя у него меньше разветвлений на каждом этапе, что улучшает типичную производительность. КМОП производительность узла процесса.
- Для сумматоров Когге-Стоуна часто проблемой является перегрузка проводки.
Приложения
Приложения сумматора Когге – Стоуна включают следующее.
- Сумматор Когге Стоуна используется в различных процессорах обработки сигналов для выполнения очень быстрых арифметических функций.
- Это расширение сумматора с упреждающим переносом, используемое для очень быстрого сложения в высокопроизводительных вычислительных системах.
- Этот тип сумматора используется в приложениях обработки сигналов.
- Этот сумматор широко используется в промышленности, главным образом, для высокопроизводительных арифметических схем.
- Этот тип сумматора обычно используется для широких сумматоров, поскольку он демонстрирует наименьшую задержку между другими структурами.
- KSA помогает добавлять большие числа, используя меньше площади, мощности и времени.
- Он широко используется в различных системах СБИС, таких как микропроцессор архитектура и архитектура DSP для конкретного приложения.
Что такое параллельный сумматор префиксов?
Параллельный сумматор префиксов — это тип сумматора, который использует операцию префикса для эффективного сложения. Эти сумматоры являются производными сумматора с упреждающим переносом и подходят для двоичного сложения посредством расширенного слова.
Какой сумматор подходит для быстрого сложения?
Сумматор с упреждающим переносом подходит для быстрого сложения в цифровой логике, поскольку этот сумматор просто увеличивает скорость за счет уменьшения количества времени, необходимого для принятия решения о переносе битов.
Что такое сумматорный алгоритм Когге-Стоуна?
Алгоритм сложения Когге-Стоуна представляет собой структуру параллельного префикса CLA, который имеет низкое разветвление на каждом этапе, что делает его более эффективным в обычных узлах процесса CMOS.
Таким образом, это обзор сумматора Когге-Стоуна Это наиболее известная версия сумматора с упреждающим переносом. Этот сумматор просто генерирует сигналы переноса за время O (log2N) и считается лучшей конструкцией сумматора. Таким образом, этот сумматор имеет наиболее распространенную архитектуру, в основном для высокопроизводительных сумматоров в отрасли. Таким образом, этот KSA имеет обычную схему и является специальным сумматором из-за наименьшего разветвления или наименьшей логической глубины. Таким образом, этот сумматор становится очень быстрым сумматором большой площади. Вот вам вопрос, что такое упреждающий сумматор?