Математика играет решающую роль в понимании поведения и работы электрические и электронные системы . Многочлены, алгебра, вероятность, интегрирование и дифференцирование и т. Д. Составляют значительную часть инструментов, используемых для решения систем. С ростом сложности систем требуются очень сложные методы. Дифференциальные уравнения широко используются для определения систем управления. Эти уравнения легко решить. Но при решении дифференциальных уравнений высшего порядка возникает сложность. Для решения таких сложных дифференциальных уравнений высшего порядка математический метод, который оказался эффективным, заключается в следующем: Преобразование Лапласа . Поскольку это преобразование широко используется, полезно знать, для чего они на самом деле предназначены и как работают.
Что такое преобразование Лапласа?
В математике преобразования применяются для преобразования переменной из одной формы в другую, чтобы упростить обработку уравнения. Преобразование Лапласа делает то же самое. Они преобразуют дифференциальное уравнение более высокого порядка в полиномиальную форму, что намного проще, чем прямое решение дифференциального уравнения.
Но есть различные преобразования, такие как преобразование Фурье, преобразование z, что делает преобразование Лапласа особенным? Основное преимущество преобразования Лапласа состоит в том, что они определены как для стабильных, так и для нестабильных систем, тогда как преобразования Фурье определены только для стабильных систем.
Формула преобразования Лапласа
Преобразование Лапласа функции f (t) во временной области, где t - действительное число, большее или равное нулю, задается как F (s), где  s - комплексное число в частотной области. s = σ + jω
s - комплексное число в частотной области. s = σ + jω
Вышеупомянутое уравнение рассматривается как односторонний Уравнение преобразования Лапласа . Когда пределы распространяются на всю действительную ось, тогда Двустороннее преобразование Лапласа можно определить как
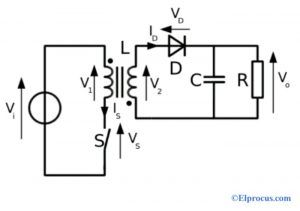
 В практических схемах вроде Цепи RC и RL Обычно используются начальные условия, поэтому для анализа применяются односторонние преобразования Лапласа.
В практических схемах вроде Цепи RC и RL Обычно используются начальные условия, поэтому для анализа применяются односторонние преобразования Лапласа.
Поскольку s = σ + jω, когда σ = 0, преобразование Лапласа ведет себя как преобразование Фурье.

Формулы преобразования Лапласа
Условия применимости преобразования Лапласа
Преобразования Лапласа называются интегральными преобразованиями, поэтому существуют необходимые условия сходимости этих преобразований.
 т.е. f должен быть локально интегрируемым для интервала [0, ∞), и в зависимости от того, является ли σ положительным или отрицательным, e ^ (- σt) может уменьшаться или расти. Для двусторонних преобразований Лапласа, а не для одного значения, интеграл сходится в определенном диапазоне значений, известном как область конвергенции.
т.е. f должен быть локально интегрируемым для интервала [0, ∞), и в зависимости от того, является ли σ положительным или отрицательным, e ^ (- σt) может уменьшаться или расти. Для двусторонних преобразований Лапласа, а не для одного значения, интеграл сходится в определенном диапазоне значений, известном как область конвергенции.
Свойства преобразования Лапласа:
Линейность

Линейность
Временной сдвиг

Временной сдвиг
Сдвиг в S-области

Сдвиг в S-области
Обратное время

Обратное время
Дифференциация в S-области

Дифференциация в S-области
Свертка во времени

Свертка во времени
Теорема о начальном значении
Теорема начального значения применяется, когда в преобразовании Лапласа степень числителя меньше степени знаменателя.  Теорема об окончательном значении:
Теорема об окончательном значении:
Если все полюса sF (s) лежат в левой половине S-плоскости, применяется теорема о конечном значении.
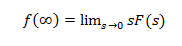 Обратное преобразование Лапласа
Обратное преобразование Лапласа
Из-за характеристики сходимости преобразования Лапласа также имеют обратное преобразование. Преобразования Лапласа демонстрируют взаимно однозначное отображение одного функционального пространства в другое. Формула обратного преобразования Лапласа:
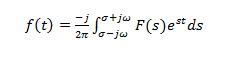 Как рассчитать преобразование Лапласа?
Как рассчитать преобразование Лапласа?
Преобразование Лапласа упрощает обработку уравнений. Когда задано дифференциальное уравнение более высокого порядка, к нему применяется преобразование Лапласа, которое преобразует уравнение в алгебраическое уравнение, что упрощает обработку. Затем мы вычисляем корни путем упрощения этого алгебраического уравнения. Теперь найдено обратное преобразование Лапласа более простого выражения, которое решает данное дифференциальное уравнение более высокого порядка.

Расчет преобразования Лапласа
Применение преобразования Лапласа
- Анализ электрических и электронные схемы .
- Разбиение сложных дифференциальных уравнений на более простые полиномиальные формы.
- Преобразование Лапласа дает информацию как об установившихся, так и о переходных состояниях.
- В машинном обучении преобразование Лапласа используется для прогнозирования и анализа данных.
- Преобразование Лапласа упрощает вычисления при моделировании системы.
Применение преобразования Лапласа в обработке сигналов
Для обработки сигналов часто используются преобразования Лапласа. Наряду с преобразованием Фурье Преобразование Лапласа используется для изучения сигналов в частотной области. Когда в сигнале в частотной области присутствуют небольшие частоты, можно ожидать, что сигнал будет плавным во временной области. Фильтрация сигнала обычно выполняется в частотной области, для которой Лаплас действует как важный инструмент для преобразования сигнала из временной области в частотную.
Применение преобразования Лапласа в системах управления
Системы управления обычно предназначены для управления поведением других устройств. Пример Системы управления может варьироваться от простого домашнего контроллера отопления до промышленной системы управления, регулирующей поведение оборудования.
Как правило, инженеры по управлению используют дифференциальные уравнения для описания поведения различных функциональных блоков с обратной связью. Преобразование Лапласа используется здесь для решения этих уравнений без потери важной переменной информации.
Характеристика линейных инвариантных во времени систем с помощью преобразования Лапласа
Для случайной системы ROC, связанной с системой, функция является правой полуплоскостью. Система анти-случайна, если ее импульсная характеристика h (t) = 0 при t> 0.
Если ROC системных функций H (s) включает ось jω, то L.T.I. система называется стабильной системой. Если случайная система с рациональными системными функциями H (s) имеет отрицательные действительные части для всех своих полюсов, то система устойчива.
Таким образом, преобразование Лапласа является важнейшим инструментом анализа схем. Можно сказать, как стетоскоп для доктора преобразования Лапласа - для инженера по контролю. Что вы считаете преобразованием Лапласа? Чем они были вам полезны?
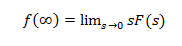 Обратное преобразование Лапласа
Обратное преобразование Лапласа 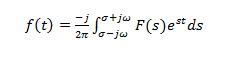 Как рассчитать преобразование Лапласа?
Как рассчитать преобразование Лапласа?